APORTACIONES DE NIKOLAS TESLA

"UNIDADES BASICAS DE UNA ONDA SENOIDAL Y SU DEFINICION" 

ONDA SENOIDAL: Es patrón de ondas que matemáticamente pueden ser descritas mediante las funciones seno y coseno. Describen acertadamente eventos naturales y señales variables en el tiempo, tales como los voltajes generados por centrales eléctricas y luego utilizados en hogares, industrias y calles.

Elementos eléctricos como resistencias, condensadores e inductancias, que se conectan a entradas de voltaje sinusoidal, producen respuestas también sinusoidales. Las matemáticas que se utilizan en su descripción son relativamente sencillas y han sido minuciosamente estudiadas.

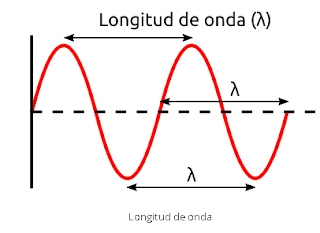
Una onda senoidal con algunas de sus principales características espaciales: amplitud, longitud de onda y fase.

Amplitud:

De acuerdo a la expresión general de la onda senoidal v (t) = vm sen (ωt+φ), vm es el valor máximo de la función, que ocurre cuando sen (ωt+φ)= 1 (recordando que el mayor valor que admite tanto la función seno como la función coseno es 1). Este valor máximo es justamente la amplitud de la onda, también conocida como amplitud pico.

En caso de tratarse de un voltaje se medirá en Voltios y si es una corriente será en Amperios. En la onda senoidal mostrada la amplitud es constante, pero en otros tipos de onda la amplitud puede variar.

Longitud de onda: 

Es la distancia entre dos crestas, entre dos valles o entre dos puntos en los que la onda tiene un valor igual a cero. Siguiendo el sistema internacional de unidades puede medirse en metros o tambien en culaquiera de sus múltiplos o submúltiplos (kilómetros, milímetros, nanómetros, etc.).

Habitualmente la longitud de onda se representa mediante la letra griega lambda (λ). .

Este parámetro puede definirse para culaquier tipo de onda periódica, incluyendo ondas de sonido, ondas de agua u ondas electromagnéticas.

Fase:

Se corresponde al desplazamiento horizontal experimentado por la onda, respecto a un tiempo tomado como referencia.

En la siguiente figura la onda verde está adelantada respecto a la roja en un tiempo td. Dos ondas sinusoidales están en fase cuando su frecuencia y su fase son las mismas. Si la fase difiere, entonces están en desfase. Las ondas de la figura 2 también están desfasadas.

Si la frecuencia de las ondas es diferente, estarán en fase cuando la fase ωt+φ sea la misma en ambas ondas en determinados instantes.

Periodo:

Una función periódica como las mencionadas, la cual se repite a intervalos regulares, cumple siempre la siguiente propiedad:

f (t) = f (t+ T) = f (t + 2T) = f (t + 3T) = ….

Donde T es una cantidad denominada período de la onda, y es el tiempo que tarda en repetirse una fase de la misma. En unidades de Sistema Internacional, el período se mide en segundos.

Frecuencia:

Es la cantidad de ciclos que ocurren en 1 segundo y se encuentra vinculada al argumento de la función seno: ωt. La frecuencia se denota como f y se mide en ciclos por segundo o Hertz (Hz) en Sistema Internacional.

La frecuencia es la cantidad inversa del período, por lo tanto:

 f = 1/T

Mientras que la frecuencia f está relacionada con la frecuencia angular ω (pulsación) como:

 ω = 2πf

La frecuencia angular se expresa en radianes /segundo en el Sistema Internacional, pero los radianes son adimensionales, así la frecuencia f y la frecuencia angular ω tienen las mismas dimensiones. Obsérvese que el producto ωt da radianes como resultado, debiendo tenerse en cuenta a la hora de utilizar la calculadora para obtener el valor de sen ωt.

Ciclo:

Es una parte de la onda contenida en un período. En la figura anterior se tomó el período midiéndolo desde dos cimas o crestas consecutivas, pero puede comenzar a medirse desde otros puntos de la onda, mientras estén limitados por un período.

Obsérvese en la siguiente figura como un ciclo abarca desde un punto hasta otro con el mismo valor (altura) y la misma pendiente (inclinación).