APORTACIONES DE NIKOLAS TESLA

 LEY DE FRESNEL

Las ecuaciones de Fresnel, son un conjunto de relaciones matemáticas que relacionan las amplitudes de las ondas reflejadas y transmitidas en función de la amplitud de la onda incidente. Su nombre hace honor al físico francés Augustin-Jean Fresnel, quien estudió el comportamiento de la luz al desplazarse entre medios que tienen índices de refracción distintos.

Ondas en una interfaz

Primero recordamos cual es la ecuación de onda para el campo eléctrico,

∇2E⃗ −1c2∂2E⃗ ∂t2=0.(1)$$\begin{array}{}\text{(1)}& {\mathrm{\nabla }}^2\overrightarrow{E}-\frac{1}{c^2}\frac{{\mathrm{\partial }}^2\overrightarrow{E}}{{\mathrm{\partial }t}^2}=0.\end{array}$$

La solución a esta ecuación es de la forma:

E⃗ =E0→cos(k⃗ ⋅r⃗ −ωt),$$\begin{array}{}\text{(2)}& \overrightarrow{E}=\overrightarrow{E_0}\cos (\overrightarrow{k}\cdot \overrightarrow{r}-\omega t),\end{array}$$

Fig. 1[1] Diagrama de onda incidente, transmitida y reflejada

Entonces para la onda incidente, la solución a la ecuación de onda se ve de la siguiente manera:

Ei→=E0i→cos(ki→⋅r⃗ −ωit),$$\begin{array}{}\text{(3)}& \overrightarrow{E_i}=\overrightarrow{E_{0i}}\cos (\overrightarrow{k_i}\cdot \overrightarrow{r}-{\omega }_{i}t),\end{array}$$

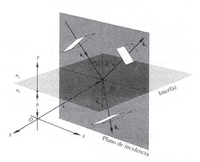
como se puede apreciar en la imagen, la onda incidente forma un ángulo con el eje normal a la interfase y por hipótesis esperamos que una parte sea transmitida y otra reflejada. El vector de onda reflejada también forma un ángulo con ese eje, de la misma manera se forma un ángulo entre el eje normal a la interfase y el vector de onda transmitida, (en un análisis posterior se observará la relación entre esos ángulos). Entonces las ondas electromagnéticas reflejada y transmitida tendrán una forma matemática similar,

Er→=E0r→cos(kr→⋅r⃗ −ωrt+ϵr),$$\begin{array}{}\text{(4)}& \overrightarrow{E_r}=\overrightarrow{E_{0r}}\cos (\overrightarrow{k_r}\cdot \overrightarrow{r}-{\omega }_{r}t+{ϵ}_r),\end{array}$$

Et→=E0t→cos(kt→⋅r⃗ −ωtt+ϵt),$$\begin{array}{}\text{(5)}& \overrightarrow{E_t}=\overrightarrow{E_{0t}}\cos (\overrightarrow{k_t}\cdot \overrightarrow{r}-{\omega }_{t}t+{ϵ}_t),\end{array}$$

donde Er${\mathrm{E}}_r$ y Et${\mathrm{E}}_t$ son constantes de fase. Ya que se analiza el comportamiento de esas ondas en la interfase, entonces podemos recurrir a la condición de continuidad para las componentes tangenciales del campo eléctrico, Eθni→|(y=b)=Eθnt→|(y=b)${\overrightarrow{E_{\theta ni}}|}_{(y=b)}={\overrightarrow{E_{\theta nt}}|}_{(y=b)}$. Para calcular las componentes tangenciales necesitamos calcular el producto cruz del vector unitario (normal a la interfase) con el campo eléctrico respectivo a cada onda,

Eθni→=u^n×E⃗ i=u^n×E⃗ 0icos(ki→⋅r⃗ −ωit),$$\begin{array}{}\text{(6)}& \overrightarrow{E_{\theta ni}}={\hat{u}}_n\times {\overrightarrow{E}}_i={\hat{u}}_n\times {\overrightarrow{E}}_{0i}\cos (\overrightarrow{k_i}\cdot \overrightarrow{r}-{\omega }_{i}t),\end{array}$$

Eθnr→=u^n×E⃗ r=u^n×E⃗ 0rcos(kr→⋅r⃗ −ωrt+ϵr),$$\begin{array}{}\text{(7)}& \overrightarrow{E_{\theta nr}}={\hat{u}}_n\times {\overrightarrow{E}}_r={\hat{u}}_n\times {\overrightarrow{E}}_{0r}\cos (\overrightarrow{k_r}\cdot \overrightarrow{r}-{\omega }_{r}t+{ϵ}_r),\end{array}$$

Eθnt→=u^n×E⃗ t=u^n×E⃗ 0tcos(kt→⋅r⃗ −ωtt+ϵt).$$\begin{array}{}\text{(8)}& \overrightarrow{E_{\theta nt}}={\hat{u}}_n\times {\overrightarrow{E}}_t={\hat{u}}_n\times {\overrightarrow{E}}_{0t}\cos (\overrightarrow{k_t}\cdot \overrightarrow{r}-{\omega }_{t}t+{ϵ}_t).\end{array}$$

Pero tanto las ondas incidentes como las reflejadas están en el mismo medio, es decir ni=nr$n_i=n_r$ entonces la suma de las componentes tangenciales del campo eléctrico incidente y reflejado, debe ser igual a la componente del campo transmitido, evaluados en y=b$y=b$, es decir la interfase,

u^n×E⃗ 0icos(ki→⋅r⃗ −ωit)|y=b+u^n×E⃗ 0rcos(kr→⋅r⃗ −ωrt+ϵr)|y=b=u^n×E⃗ 0tcos(kt→⋅r⃗ −ωtt+ϵt)|y=b.$$\begin{array}{}\text{(9)}& {\hat{u}}_n\times {\overrightarrow{E}}_{0i}\cos (\overrightarrow{k_i}\cdot \overrightarrow{r}-{\omega }_{i}t){|}_{y=b}+{\hat{u}}_n\times {\overrightarrow{E}}_{0r}\cos (\overrightarrow{k_r}\cdot \overrightarrow{r}-{\omega }_{r}t+{ϵ}_r){|}_{y=b}={\hat{u}}_n\times {\overrightarrow{E}}_{0t}\cos (\overrightarrow{k_t}\cdot \overrightarrow{r}-{\omega }_{t}t+{ϵ}_t){|}_{y=b}.\end{array}$$

Para establecer una relación entre las fases de los cosenos, tenemos que tomar en cuenta que eso solo puede ser posible para cualquier punto en la interfase, y para todo tiempo, entonces de esa manera podemos establecer una igualdad entre fases:

(ki→⋅r⃗ −ωit)|y=b=(kr→⋅r⃗ −ωrt+ϵr)|y=b=(kt→⋅r⃗ −ωtt+ϵt)|y=b,(10)$$\begin{array}{}\text{(10)}& (\overrightarrow{k_i}\cdot \overrightarrow{r}-{\omega }_{i}t){|}_{y=b}=(\overrightarrow{k_r}\cdot \overrightarrow{r}-{\omega }_{r}t+{ϵ}_r){|}_{y=b}=(\overrightarrow{k_t}\cdot \overrightarrow{r}-{\omega }_{t}t+{ϵ}_t){|}_{y=b},\end{array}$$

de la anterior relación, las frecuencias de la fases reflejada y transmitida se verán forzadas a obtener el mismo valor que la frecuencia de incidencia, esto se debe a que la onda incidente hace vibrar los electrones de los medios dieléctricos de manera forzada, por lo tanto ωi=ωr=ωt${\omega }_i={\omega }_r={\omega }_t$ por consiguiente llegamos a:

(∗)(ki→⋅r⃗ )|y=b=(kr→⋅r⃗ +ϵr)|y=b=(kt→⋅r⃗ +ϵt)|y=b.(11)$$\begin{array}{}\text{(11)}& (\ast )(\overrightarrow{k_i}\cdot \overrightarrow{r}){|}_{y=b}=(\overrightarrow{k_r}\cdot \overrightarrow{r}+{ϵ}_r){|}_{y=b}=(\overrightarrow{k_t}\cdot \overrightarrow{r}+{ϵ}_t){|}_{y=b}.\end{array}$$

Apartir de la relación anterior (∗$\ast$)se verá que sucede con las constantes de fase. Tomemos la primera igualdad y despejemos la constante de fase,

ϵr=(ki→⋅r⃗ −kr→⋅r⃗ )|y=b=(ki→−kr→)⋅r⃗ |y=b,(12)$$\begin{array}{}\text{(12)}& {ϵ}_r=(\overrightarrow{k_i}\cdot \overrightarrow{r}-\overrightarrow{k_r}\cdot \overrightarrow{r}){|}_{y=b}=(\overrightarrow{k_i}-\overrightarrow{k_r})\cdot \overrightarrow{r}{|}_{y=b},\end{array}$$

pero recordemos que el plano en el que habitan los vectores de onda (plano de incidencia) es ortogonal al plano del vector de posición (plano de interfase), entonces el producto punto entre ellos será cero, por lo tanto ϵr=0${ϵ}_r=0$, una vez establecido esto, podemos escribir,

(ki→−kr→)=0,(13)$$\begin{array}{}\text{(13)}& (\overrightarrow{k_i}-\overrightarrow{k_r})=0,\end{array}$$

calculando el producto cruz del vector unitario con esa resta vectorial,

u^n×(ki→−kr→)=0,(14)$$\begin{array}{}\text{(14)}& {\hat{u}}_n\times (\overrightarrow{k_i}-\overrightarrow{k_r})=0,\end{array}$$

recordemos que la magnitud del producto cruz de dos vectores es igual al producto de sus magnitudes veces el seno del ángulo entre ellos, entonces la ecuación anterior queda de la siguiente manera:

kisinθi−krsinθr=0,$$\begin{array}{}\text{(15)}& k_i\sin {\theta }_i-k_r\sin {\theta }_r=0,\end{array}$$

reacomodando términos,

kisinθi=krsinθr,$$\begin{array}{}\text{(16)}& k_i\sin {\theta }_i=k_r\sin {\theta }_r,\end{array}$$

pero recordemos como se define k$k$, k=ωnc$k=\frac{\omega n}{c}$, como las frecuencias son iguales, y la velocidad de la luz es constante, la relación queda en función de los ángulos y de los índices de refracción de los medios:

nisinθi=nrsinθr,$$\begin{array}{}\text{(17)}& n_i\sin {\theta }_i=n_r\sin {\theta }_r,\end{array}$$

ahora se puede observar que nr=ni$n_r=n_i$ por lo tanto factorizando el término común llegamos a lo siguiente:

θi=θr,(18)$$\begin{array}{}\text{(18)}& {\theta }_i={\theta }_r,\end{array}$$

que es la relación de reflexión, dicha relación será de utilidad en análisis posteriores.

De la relación ∗$\ast$ se tomará ahora la segunda igualdad, es decir se realizará el análisis para la parte incidida y transmitida,

(ki→⋅r⃗ )|y=b=(kt→⋅r⃗ +ϵt)|y=b,(19)$$\begin{array}{}\text{(19)}& (\overrightarrow{k_i}\cdot \overrightarrow{r}){|}_{y=b}=(\overrightarrow{k_t}\cdot \overrightarrow{r}+{ϵ}_t){|}_{y=b},\end{array}$$

ahora despejemos ϵt${ϵ}_t$

ϵt=(ki→⋅r⃗ −kt→⋅r⃗ )|y=b=(ki→−kt→)⋅r⃗ |y=b,(20)$$\begin{array}{}\text{(20)}& {ϵ}_t=(\overrightarrow{k_i}\cdot \overrightarrow{r}-\overrightarrow{k_t}\cdot \overrightarrow{r}){|}_{y=b}=(\overrightarrow{k_i}-\overrightarrow{k_t})\cdot \overrightarrow{r}{|}_{y=b},\end{array}$$

tal como en el caso anterior, el producto punto entre estos vectores será cero, lo que implica que ϵt=0${ϵ}_t=0$, entonces se puede escribir

(ki→−kt→)=0,(21)$$\begin{array}{}\text{(21)}& (\overrightarrow{k_i}-\overrightarrow{k_t})=0,\end{array}$$

y calculando el productor cruz de u^n${\hat{u}}_n$ con la resta de vectores anterior

u^n×(ki→−kt→)=0,(22)$$\begin{array}{}\text{(22)}& {\hat{u}}_n\times (\overrightarrow{k_i}-\overrightarrow{k_t})=0,\end{array}$$

de esta operación obtenemos

kisinθi−ktsinθt=0,$$\begin{array}{}\text{(23)}& k_i\sin {\theta }_i-k_t\sin {\theta }_t=0,\end{array}$$

como en el caso anterior, se dejará la ecuación en términos de los índices de refracción y los ángulos

nisinθi=ntsinθt,$$\begin{array}{}\text{(24)}& n_i\sin {\theta }_i=n_t\sin {\theta }_t,\end{array}$$

la anterior ecuación encontrada recibe el nombre de relación de Snell, tanto ella como la relación de reflexión nos ayudarán a hacer los análisis siguientes, en los cuales se mostrarán los índices de reflexión y transmisión para campo eléctrico ortogonal y paralelo al plano de incidencia.